

The headings and some of the text have mouse-over effects to liven up the page.
Those effects are independent of your browser's copy-paste functionality.
If you intended to send an excerpt from this page to your wife but mistakenly sent her a prior text intended for your mistress, that is on you not me.
I have not decided whether this page will contain advertising.
The core content of this page takes up even most desktop screens, but one or more advertisements created by skilled graphic artists might enhance the existing text only layout.
Even without advertising and with some simplifying assumptions, it is difficult to present this much information even on a laptop or desktop screen.
On a cellphone screen it is that much more challenging.
To mitigate that, there are some navigation buttons below with which you can jump to sections within this page.
This page will introduce the concept of credit card interest as typically applied in the United States.
The page following this page will cover the subject of statement cycles.
For those of you outside the United States, I have no idea how any of this information may or may not apply to you.
For those of you that do reside in the United States:
A credit card's annual percentage rate refers to the interest that would be charged over the course of a year.
If you only buy goods and services and you always pay your statement balance in full by your due date, then explaining how the annual percentage rate will impact you is easy.
You will not owe interest.
You will have a grace period with no interest charged if you pay the entire statement balance by your due date.
In this context grace period does NOT mean paying your credit card after the due date.
Grace period means you will not accrue interest because you have been paying in full.
That is the explanation.
If you do any one or any combination of the following, then the explanation becomes more complicated:
If you perform any of the above then you may be charged interest.
Even then, if you are within a 0% interest promotion period for a card then you might not be charged interest.
If you have a promotional interest rate then that promotional rate might apply to just:
For-profit banks typically do charge balance transfer fees and fees for cash advances.
If you use a 0% promotional interest rate that is only for balance transfers you will likely lose your grace period for new purchases.
That means that while you will not be charged interest for the balance transfer, you will be charged interest for purchases.
You will need to understand the terms for your specific card or cards.
The intent of this page is to be a gentle introduction to understanding credit card interest.
According to dictionary.com, the origin of the word percentage is the Latin phrase by the hundred.
If you begin the year with a $10,000 balance on a credit card account that has a 22% interest rate, make no additional purchases, balance transfers or cash advances, and just pay the interest each month, how much interest would there be over the course of the year?
Ignoring possible daily compounding of interest that I will cover in the next section, that means $22 per $100.
Divide $22 and $100 each by 100 leaving us with $.22 per $1.
How many multiples of 1 do we have?
We have 10,000 multiples of 1.
Our interest would be .22 times $10,000 for a total of $2,200 of interest.
In any one month, you would be charged roughly 1/12 of that for $2,200/12, about $183.33 interest.
As a nod towards completeness, I am going to touch on compound interest in this section but you may actually feel quite free to skip to the next section.
Understanding the difference between simple interest as you might envision it and compound interest as it applies to credit cards is like understanding the difference between being attacked by a chimpanzee and being attacked by a gorilla.
In either case, it is very much in your best interest to anticipate the danger well in advance and ideally avoid it all together.
If you are carrying a balance on your credit card and a 0% interest promo does not apply then interest will accrue on your balance.
It is actually somewhat worse than you might think because for your credit card there is a very strong chance that if interest is accruing, that interest is compounded.
Being charged compound interest means that you are being charged interest on your interest.
If you are an investor buying a pool of a credit card receivables then understanding how credit card interest compounding may be critical.
For the average consumer, whether you are carrying a large balance at 22% per year or whether the true cost is higher than 22% when compound interest is taken into account, you are in trouble either way.
Still reading?
OK, well I will briefly go over credit card compound interest.
Assume for this example that the annual percentage rate on your credit card is 22 percent as in the explanation several lines above.
From your annual percentage rate we calculate your daily periodic rate.
Your daily periodic rate is .22 / 365, giving us value of 0.00628571428
Hmmm, $10,000 times 0.000602739726027397 times 365 yields the same $2,200 value we calculated earlier.
So what exactly was the point of calculating the daily periodic rate??
if you are carrying a balance, with some credit card issuers your balance may compound interest daily.
You will be paying interest on your interest.
Plausible Representation Of Daily Compounding
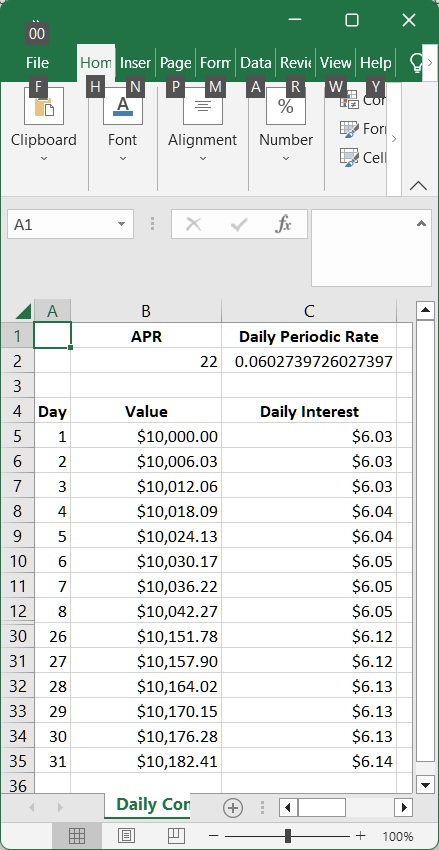
For brevity, I hid days 9 through 25 before creating the graphic from Excel.
As you can see in column C, the interest per day is slowly growing.
Possible daily compounding of interest is something to be aware of, but I am skeptical of daily compounding being the issue that caused someone to become unable to pay his or her credit cards.
In the interest of simplicity, in the exercises to follow, please assume that no credit cards have daily compounding of interest.
I am not saying ignore credit card interest, I am saying ignore potential daily compounding of interest.
Setting up even a small number of exercises intended to each have exactly one correct answer that can withstand the scrutiny of the internet is terrifying.
You were furloughed from your job in April 2020.
You began working again in November of 2020.
At the beginning of 2022 you had a credit card with a balance of $18,000.
The interest rate on the credit card is 19%.
You did not make any purchases, balance transfers, or cash advances on the account during 2021 or 2022.
You have always made your payments on time, but since the start of your furlough through the present you have only been paying the minimum due by the payment due, which was the interest only.
In real life the minimum payment due each month will likely include some principal, but if I allow for paying principal in addition to interest then setting up this exercise becomes more difficult.
Also in real life, a credit card interest rate will usually be tied to some benchmark that varies, but for simplicity let's assume that your interest rate on the entire balance was a constant 19% throughout the year.
Which answer equals or is at least closest to the cost of that interest in the preceding scenario over the course of the year 2022?
A) $180
B) $190
C) $1,980
C) $3,420
D) $7,240
The answer is: C) $3,420.
How did I arrive at that answer?
$18,000 times .19 equals $3,420.
Starting with our answer from the previous exercise for the annual interest, what will be the interest for any one random month?
The answer I am looking for is $3,420/12 for a monthly interest of $282.
If you allow for additional purchases between your statement open and statement close dates and daily compounding, the math can be more complicated.
You have 2 credit cards: credit card A and credit card B.
Applies To Card A
Credit card A has a limit of $15,000 and an interest rate of 17%.
You had some financial setbacks during the last few years, resulting in card A having a balance of $7,500
You have made all your payments on time but in no month have you paid your entire statement balance off since before the start of the Covid19 era.
Applies To Card B
Credit card B has a limit of $15,000 and an interest rate of 22%.
Credit card B does not currently have a balance.
On credit card B you have never done any of the following:
Applies To Both Cards
Neither card has any kind of promotional rate in effect nor is any available.
Assume that today is the first day of the current month.
Both cards have a statement opening date of the first of this month and a statement closing date the last day of this month.
Both cards have a payment due date of the 21st of next month.
Neither card offers cash back or any kind rewards on purchases.
You must pay for an unexpected expense of $5,000 today.
You are absolutely certain that you will have a deposit in your checking account for $5,000 which will have fully cleared a week before your payment is due next month, but in order to pay today as needed you will use a credit card.
Narrowly for this question, if your goal is to minimize paying the total interest between the two cards, should you put the $5,000 charge on card A or card B?
For whatever balance or balances the $5,000 deposit does not pay down, you will make minimum payments until you receive your bonus from work several months from now.
To get credit for this exercise, you must not merely state the correct card but you must be able to explain your reasoning.
It may or may not be surprising, but in the scenario above if your goal is to minimize total interest between the two cards you would put the charge on card B that has the 22% interest rate.
Why?
Because as long as you can pay the statement balance for card B by the payment due date, since you have not been carrying a balance, there will be no interest charged on card B.
You are carrying a balance on card A so you have lost the grace period that you have on card A.
If I had typed Exercise 3: Grace Period instead of Exercise 3: { Guess The Intended Theme After Solving The Exercise } at the beginning of this exercise that might have made the question too easy.
In the year 2023 what financial asset or assets can you invest in that will provide a guaranteed annual return of 22% or more?
A credit card issuer may lend money at 22% or even higher.
Out of that interest the bank has to pay not only its admittedly small cost of deposits but also for its employees and overhead such as office space.
Even with an aggressive and effective collections effort, some percentage of not mere interest but outright principal will prove to be uncollectible.
Be extremely wary of predictions from me or anyone else.
I would be not just surprised but rather completely shocked if I were proven wrong with the following prediction:
From now until the end of humanity, large numbers of people will lose large amounts of money because they did not understand red flags in investment scams that are sent by scammers on dating sites and social media.
This page included four exercises intended to test your understanding of credit card interest and interest in general.
As long as you are remembering the process, not simply the text of the answer, returning later to review this same small set of exercises can have value.
Even if you did not learn anything new, the exercises might still have helped reinforce what you already knew.
In the years to come, people will find themselves being in anywhere from moderate to extreme financial danger because they could not grasp the lessons on this page.
On its own, being able to answer Exercise 4 correctly won't allow you to retire as a wealthy man or woman, but it may mean one less person that falls victim to one or more online scams.